

When Poisson’s ratio is no longer valid, we cannot calculate the cross-section by using the Poisson’s ratio. Once the plastic deformation starts, Poisson’s ratio, which defines the relationship between longitudinal and lateral strains, is no longer valid. True stress is used in the plastic region where the elongation is fairly increased. When a material is stretched and its strain increases, plastic deformation starts to occur.
When is the change in cross-sectional area significantly large? We are considering about this with respect to the stress-strain diagram mentioned earlier. So, the true stress is used only when the change in cross-section area is large. When the change in the cross-section area is small, the behavior of the material can be well approximated by using the nominal stress. The true stress is the load divided by the real cross-section area of a moment. Following argument includes this point, situations in which nominal stress and true stress should be used respectively. After getting familiar with this explanation, you may think that the stress, or nominal stress, which we have been using, is a bit rough.
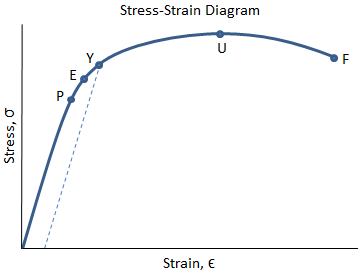
The quantity, which we have called “stress” so far, has been the “nominal stress”. This stress is called the true stress defined by the following equation. You may notice that we need to divide the load, P, by the reduced cross-section area, A, in order to calculate the stress more precisely. Here, A0 is the initial cross-section and A is the cross-section at a moment during the defamation. We may here recall the story of the Poisson’s ratio, which also argued about the reduction of cross-section area due to the stretch of a bar. The following illustration describes the deformation of a bar stretched from the initial length of L0 to final length of L at force P. However, if you stretch a material up to a fairly higher strain, the material becomes thinner significantly reducing the cross-section area. This stress is called the “nominal stress”. This value has been defined as “stress” and various problems were solved based on this definition. In the previous argument, the external load was divided by this original cross-section area A0 to calculate the stress. Now, we assume that the original cross-section area is A0 in which any load is acting on the material. The cross-sectional area changes as a function of time as the material is stretched. In reality, however, the calculation is not strict. You may notice that the cross-section area here is actually the area under no load acting on it. We learned that when calculating a stress in a material, the load applied to the material should be divided by the cross-section area. The true stress is a little different from the stress that we have argued so far.


 0 kommentar(er)
0 kommentar(er)
